Getting asked to graph an equation like this
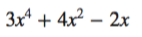
may at first seem a bit daunting.
No need to fear, in this article you will learn exactly how to do it!
A polynomial is any expression in the form
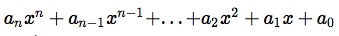
where,
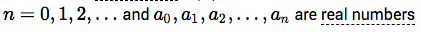
So, for example, linear, quadratic and cubic expressions are all forms of polynomials that you may have worked with before.
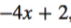
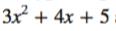
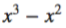
When it comes to sketching a polynomial, the easiest way to do it is by finding the x- and y-intercepts.
The y-intercept is usually the easiest one to find. Just substitute x=0 into the equation, and the output value is the y-intercept.
The x-intercept is usually the more challenging one to find as there are multiple solutions. The following steps will take you through how to find the x-intercept.
To find the x-intercepts and then graph the polynomial,
1. Write the polynomial in factored form. In the example below, x was factorised first, leaving a quadratic, which was then factorised to give the final line.

2. Equate the polynomial to zero. The x-intercepts become the value of x that make the equation equal to zero. In the example above, that would be -2,0 and 4. These are the x-intercepts.
3. Once you have the x-intercepts, find the y-intercept. In the example above, the y-intercept is 0.
4. Then, plot these points on a Cartesian plane. Test for a point greater than the biggest x-intercept. This will tell you the behaviour of the graph after the x-intercept, and hence where to start (above or below the x-axis). In this example, I tested for x=8 and got a y-value of 320. This means after x=4; the function is above the x-axis. (Alternatively, you could test for an x-value less than the smallest x-intercept.)
5. Then start at the point (8,320). Come down to the first intercept (x=4), and then turn around to go up to x=0, then back down again to x=-2. The function continues towards negative infinity. This is the resulting graph.

To watch the video of the graphing of this polynomial, check out this video!
If you found this helpful and struggle with other Function related concepts, check out the online Functions- Mathematics Advanced HSC Course.
This course goes through the complete Functions Mathematics Advanced syllabus in just a few hours. It includes videos and quizzes to help your understanding and consolidation of concepts.
This is a great tool for any student (Year 10,11,12) looking to learn this topic ahead of the class, close gaps in their learning, and revise it.
For more information and to sign up for a free preview of the course, click the following link.
If you have any questions, don't hesitate to contact me using this form or on my socials:
Instagram/Facebook @compassmathstutoring.
I hope you found this helpful!
Good luck with the rest of your studies!

Comments