"Reducing-balance loans" are calculated on the balance owing which changes every time a repayment is made. This is different to a "flat-rate loan" that calculates interest on the initial amount of money borrowed.
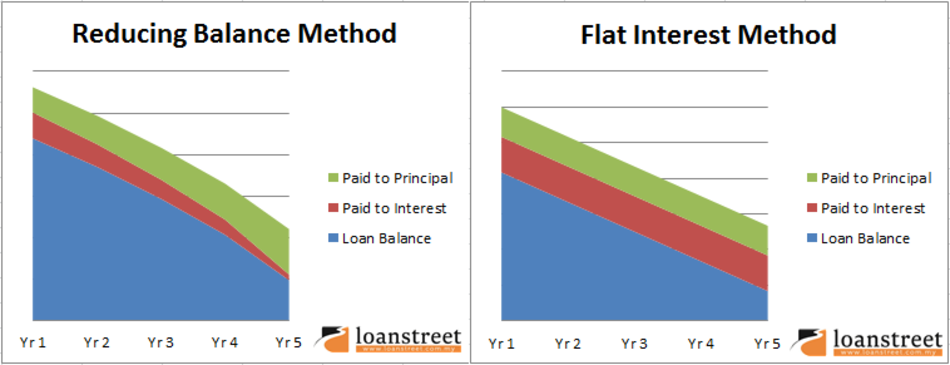
As you can see on the graph below, a reducing-balance loan is curved, whereas the flat interest loan is linear (straight). You can use this point of difference when comparing graphs of reducing balance loans and flat interest loans.
This is because as payments are made on the loan, the balance decreases, and so the interest charged decreases. This means that you can pay off a loan faster with the reducing balance method than the flat interest method, provided that the initial amount borrowed is the same.
The calculations for reducing-balance loans are complicated, and so you will often use tables made by financial institutions to assist with calculations.
For example, the table below shows the monthly repayments of a reducing-balance loan. The question asks you to find the interest to be paid on a loan of $150,000 over 12 years.
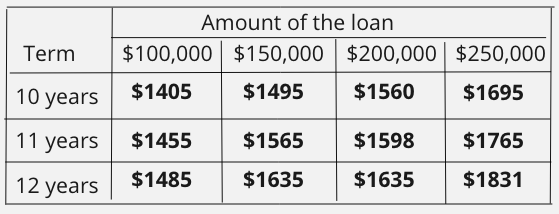
1. The first thing is to find the intersection of the loan and the period of repayment.
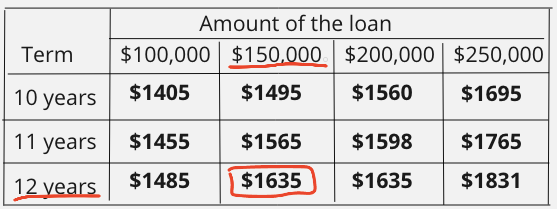
This gives us a monthly repayment of $1635.
2. Then find the period of repayment by multiplying the 12 years by 12 to get months= 144 months.
3. Multiply the 144 months by the monthly repayment of $1,635= $235,440. This is how much you will pay back over the 12 years.
4. To find interest, subtract the amount borrowed ($150,000) by this amount ($235,440)= $235,440 - $150,000= $85,440. This is the interest on the loan.
For a more in-depth explanation, check out this video!
If you found this helpful and struggle with other financial mathematics concepts, check out the online Financial Mathematics- Mathematics Standard 2 HSC Course.
This course goes through the complete Financial Mathematics Mathematics Standard 2 syllabus in just a few hours. It includes videos and quizzes to help your understanding and consolidation of concepts.
This is a great tool for any student (Year 10,11,12) looking to learn this topic ahead of the class, close gaps in their learning, and revise it.
For more information and to sign up for a free preview of the course, click the following link.
If you have any questions, don't hesitate to contact me using this form, or on my socials:
Instagram/Facebook @compassmathstutoring.
I hope you found this helpful!
Good luck with the rest of your studies!
Kommentare